抵抗計算
これから抵抗の計算について頭に入れていただきたい。回路図と数式がありますね〜
このような回路をはじめてみた方、もう見たことあるよ!って方が大半ではないでしょうか?
このような回路方式を直並列接続と言います。
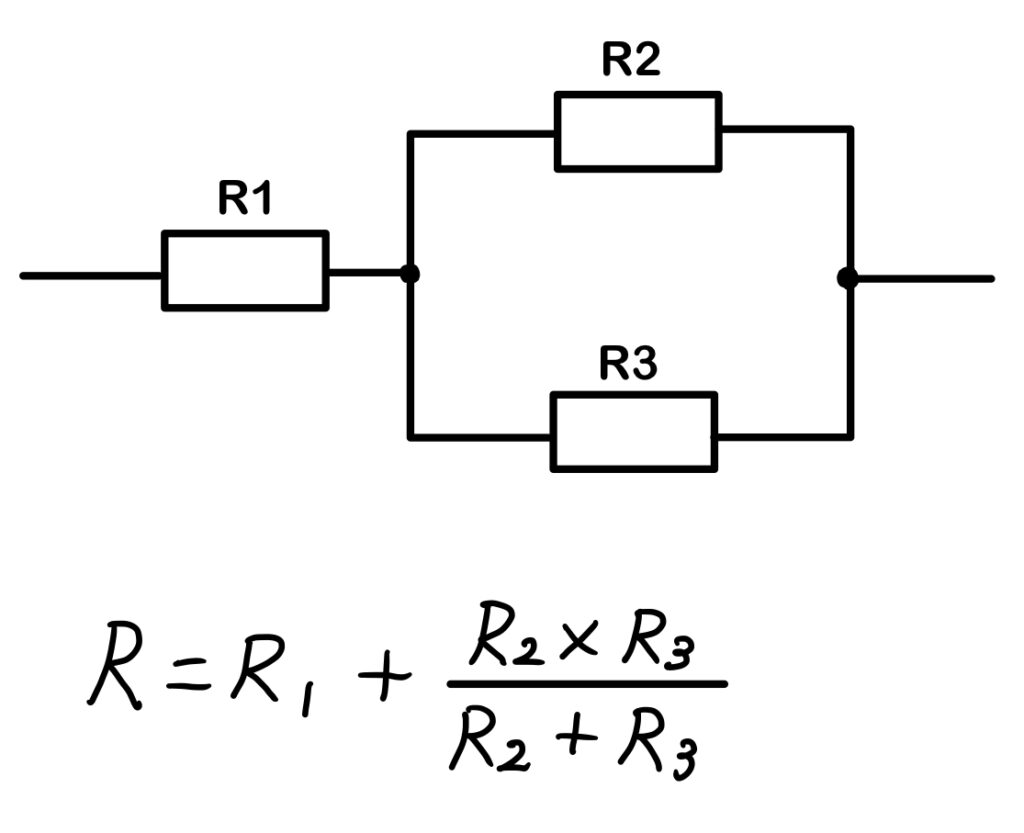
と、言われても直列って何?並列って何?ってなった方もいると思います。この回路は私が大学1年で1回目の電気理論の講義でこの回路を数式で示せと言われ
なんじゃいこれわあああああああああ
ってなったのを今でもブログを書きながらイマジネーションしてます。これから直列接続、並列接続について見ていきましょう。
直列接続
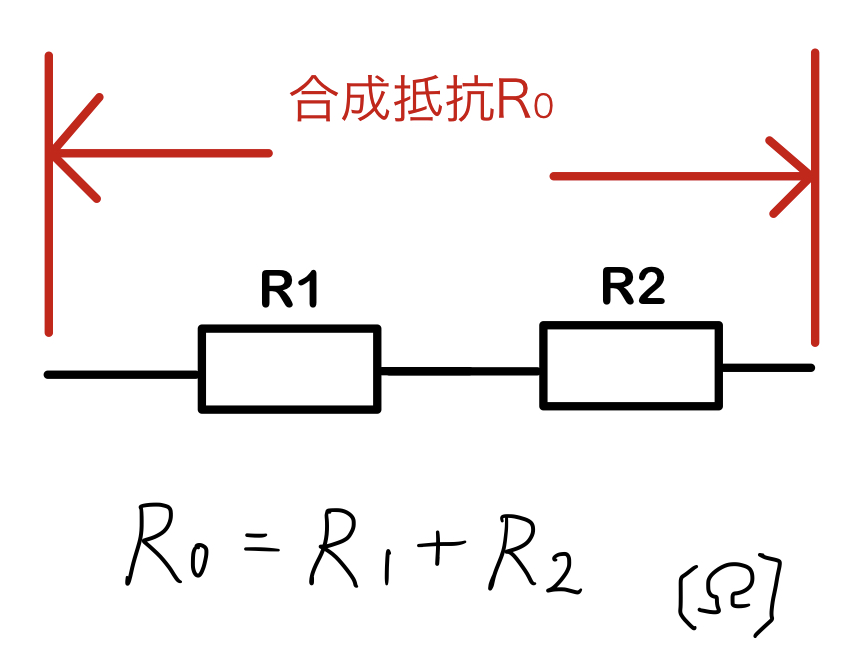
それでは直列接続について見ていきましょう!図2に示します。
見ての通り
足し算です。また、数式を見ると「R0:アールゼロ」というのがあるのですがこれは合成抵抗と言います。
例えば 1+1=2 は 2=1+1 とも表せますようね この「2」の部分を合成抵抗値、算数だと合計(ゴウケイ)になるわけです。つまり、R1=1Ω、R2=1Ωの時合成抵抗R0は?って言われた時にはR0=2Ωとなるわけです。
 Sunn
Sunn並列接続
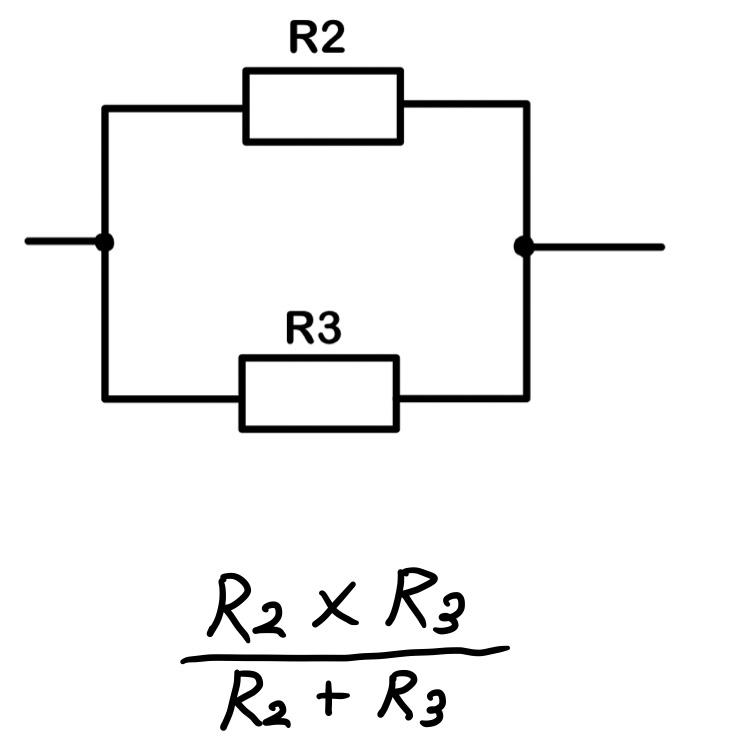

次に並列接続について見ていきましょう!図3に示します。
数式を見るとおやおや、、なんじゃこれ 分数やんんん 俺分数大っ嫌いなんだー
って頭の脳裏を無限ループしてますよね。。。大丈夫私もそうでした!
抵抗2つの時だけとある必殺技をくりだすことができます、通称、、、
和分の積攻撃
分母を見てください 足し算になっている! 分子を見てください掛け算になっております。
なんていうこことでしょう。頭の中で抵抗2つの時は和分の積と覚えておけばいいのです。
しかし次のような回路が来た時どう対処していけばいいのでしょうか、、、
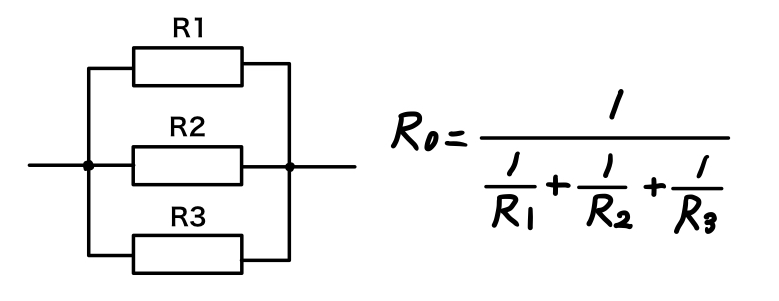

抵抗が3つになっているし数式もまたわけわからんものが立ちはだかりました。おそらく参考書を買うとまず書いてある数式だと思います。でも大丈夫私には和分の積攻撃ができるのであるから。R1とR2にだけに注目すると、、
これ和分の積攻撃使えるんじゃね❓ってなります。そーーーなんです使えちゃうんだすよ!
和分の積攻撃をするとさらに以下のように回路変換できます。
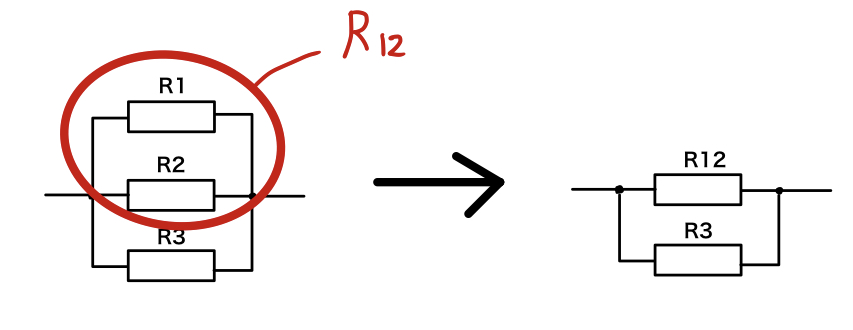

これでまた再度和分の積攻撃すれば合成抵抗が求まるわけですね。
例えば図3においてR1=2Ω、R2=2Ω、R3=3Ωだったら、まずR1とR2の合成抵抗R12を和分の積攻撃で求めると
R12=1Ωとなって再度R12とR3の和文の積をすれば合成抵抗R 0=0.75Ωとなるね!
(じゃあ抵抗が数百個出てきたら同じことするの?と言われがちですがそもそも第二種電気工事士試験ではそんな問題出てきませんし、大丈夫です。本ページでは抵抗計算をイマジネーションして欲しいから、、、)
もっと簡単に効率よく解ける方法はいくらでもありますが電験ではないので大丈夫です!



ここまで理解できたら図1の直並列接続回路も解けてしまうのでは?実際に自分でR1、R2、R3の値を決めて合成抵抗R0を求めてみよう!
試験問題にチャレンジ
それではまとめとして図6のような回路で、端子ab間の合成抵抗を求めてください!
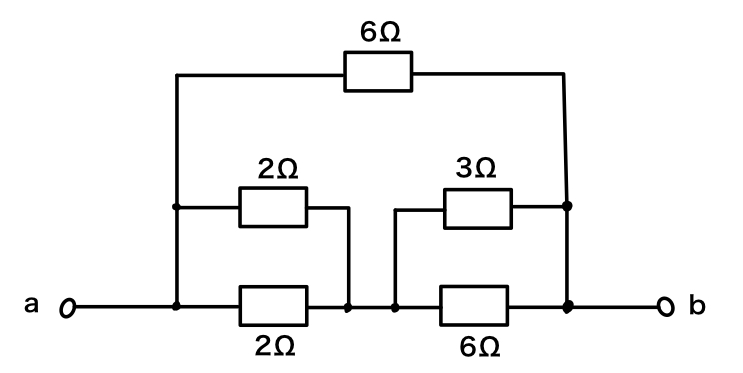

解答解説はのちほどYouTubeチャンネルで公開しますね!
今回は抵抗計算について解説しました!これからもどんどんブログ記事を公開していくのでよろしくお願いします!






